《小数乘整数》教学设计之一—

了解站长

关于本站

返回老站

中国桥站

　　老百晓在线

第九册

小数乘整数

教学设计

	作者：佚名
	《小数乘整数》教学设计之一

　　教学内容：人教版小学数学教材五年级上册第2～3页例1、例2及“做一做”，练习一第1～5题。
　　教学目标：
　　1.使学生理解小数乘整数的算理，掌握小数乘整数的一般方法，会比较熟练地进行笔算。
　　2.使学生经历将小数乘整数转化为整数乘整数的过程，自主探索小数乘整数计算方法的过程，渗透转化的数学思想，培养简单的逻辑推理能力。
　　3.使学生体会小数乘法在实际生活中的应用，感受数学源于生活，生活需要数学，形成积极的学习态度。
　　教学重点：掌握小数乘整数的一般计算方法。
　　教学难点：理解小数乘整数的算理。
　　教学准备：课件。
　　教学过程：

　　一、情境引入，提出问题
　　（一）课件呈现，寻找信息
　　1.课件呈现“放风筝”的情境以及各种不同形状的风筝。
　　2.课件呈现“买风筝”的情境（例1的主题图），画面上醒目地显示四种形状各异、价格不同的风筝。
　　3.设问：从图中你能看出哪些数学信息？
　　（二）提出问题，揭示课题
　　1.这节课我们就一起先来解决“买3个蝴蝶风筝多少钱”的问题，你能列出算式吗？（教师板书或PPT课件呈现：3.5×3＝）
　　2.追问：这个算式和我们以前学过的算式有什么不同呢？
　　3.引导：今天我们就来学习小数乘整数。（板书课题：小数乘整数）
　　二、自主尝试，感悟算理
　　（一）感知算理
　　1.算一算：3.5×3，可以怎样计算？
　　　给足时间，让每一位学生根据自己的知识和经验独立计算出买3个蝴蝶风筝所需的钱数。教师巡视，注意发现学生中的不同计算思路。
　　2.说一说：你是怎样计算的？
　　　学生的计算思路可能有：用加法进行计算；改写为复名数进行计算；化“元”为“角”进行计算等。
　　（二）重点分析、研讨化“元”为“角”算法的算理
　　1.组织全班学生对上述多种不同解法逐一进行分析、评价和充分肯定。
　　2.引导学生着重分析化“元”为“角”的计算方法。
　　（1）师：上述几种算法中，你认为哪种算法比较简单？这种算法中的关键是什么？
　　（2）学生分析、对比、讨论后，引导学生用简洁的话总结、概括：先把3.5元转化为35角，再计算35角×3，最后将结果105角转化成10.5元。
　　（3）教师边小结边适时板书（或PPT课件动态呈现）如下竖式计算过程：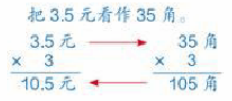
　　　

　　（4）小结：刚才我们在解决“买3个蝴蝶风筝多少钱”的问题时，想到了各种不同的计算方法。我们发现以“元”作单位的小数乘整数，可以转化成以“角”（或“分”）作单位的整数乘整数来进行计算。
　　【设计意图】依托现实情境，让学生利用已有的知识经验，用自己理解的方法自主解决问题。在充分肯定学生的其他合理方法之后，着重分析和评价化“元”为“角”的算法，引导学生总结、概括这种算法的思考过程，体会小数乘法和整数乘法的联系，感受小数乘整数还可以转化成整数乘整数进行计算，初步感悟小数乘整数的算理和算法，培养学生的数学思维能力。
　　（三）巩固化“元”为“角”的计算方法
　　1.第2页“做一做”第1题。
　　（1）学生独立完成，教师指名演板。
　　（2）重点评价“把4.6元看作46角”进行计算的方法。
　　2.第2页“做一做”第2题。
　　（1）学生独立完成。
　　（2）组织学生交流解决问题的思路和方法（主要关注下面两种方法）。
　　　方法一：先算出具体的钱数6.4元×7＝44.8元，再与40元进行比较，做出判断。
　　　方法二：直接通过估算解决，一个燕子风筝的价格是6.4元，超过了6元，买7个就超过了42元，所以40元不够。
　　（3）拓展：50元够吗？
　　三、运用转化，探究算法
　　（一）动态呈现小数乘整数的过程
　　1.出示算式0.72×5＝?，提问：“0.72不是钱数，怎样计算？”
　　2.让学生独立思考，再引导学生提出：“能不能转化成整数来计算？”
　　3.学生尝试列竖式计算。（教师巡视，了解学生的计算方法。）
　　4.小组交流计算方法。
　　5.学生全班集体交流转化过程和计算方法，教师适时板演（或PP课件演示）乘法竖式计算过程，帮助学生理解算理算法。
　　（教师重点引导学生理解三点：怎样把因数0.72转化成整数？乘得的积应如何处理？积末尾的“0”如何处理？从而使学生更好地理解算理。）
　　　由于因数0.72化成整数72必须“×100”，所以要使积不变，积360应“÷100”。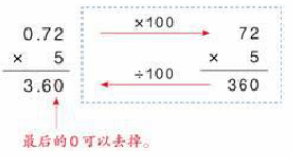
　　　

　　（二）将乘得的积化成最简小数
　　　请学生观察乘得的积“3.60”，提问：3.60是最简小数吗？（不是！）提醒学生，乘得的积如果不是最简小数，可以根据小数的基本性质将积中小数末尾的0去掉。
　　（三）小结小数乘整数的一般方法
　　1.引导学生回顾3.5×3、0.72×5的计算过程。
　　2.提问：“想一想，在计算小数乘整数时，你先做什么？再做什么？最后又做什么？”
　　3.引导学生在理解的基础上归纳小数乘整数的一般方法：
　　（1）先将小数转化为整数；
　　（2）按整数乘法算出积；
　　（3）再确定积的小数点位置。（因数有几位小数，就从积的右边起数出几位，点上小数点。若积的末尾有“0”，末尾的“0”可以去掉。）
　　四、拓展应用，巩固新知
　　（一）专项练习
　　1.小数乘整数与整数乘整数的对比。（第3页“做一做”第1题）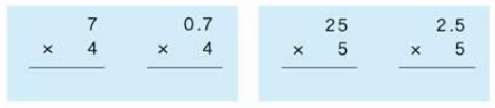
　　　

　　　想一想：小数乘整数与整数乘整数有什么不同？
　　（1）引导学生审题，明确题目要求，学生独立完成。
　　（2）组织学生交流、讨论，归纳小数乘整数与整数乘整数的不同：小数乘整数中有一个因数是小数，整数乘整数中两个因数都是整数；小数乘整数的积中，若小数末尾有0，这个0可以去掉，但整数乘整数的积末尾的0不能去掉。
　　2.确定积的小数点。（第3页“做一做”第2题）
　　　

　　（1）学生独立完成。
　　（2）组织学生交流：你是怎样确定积的小数点的位置的？积末尾的0是怎样处理的？
　　（三）趣味练习（智慧岛）
　　1.小狗登城堡。
　　　

　　2.小金鱼戏水。
　　　

　　3.小蜜蜂采蜜。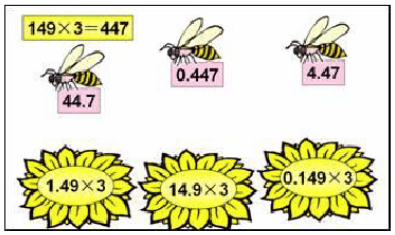
　　　

　　（四）应用练习
　　1.练习一第3题。
　　（1）引导学生正确用合适的方法估计自己家到学校的路程。如：用步测的方法估计，知道自己的步长约为0.6?m，从自己家到学校约走多少步，用步长0.6?m乘走的步数，就得到自己家到学校的大致路程。
　　（2）通过计算自己每天、每周上学要走的路程，巩固小数乘整数的计算方法，加深对一千米有多长的具体的感受。
　　五、课堂总结，深化新知
　　　这节课我们学到了什么？你是怎么学会的？
　　六、课外作业
　　　做一做的第三题。练习一第1、4、5题。

[2020-08-20]

　摘自《百度文库》网站


	上一篇
	下一篇