《倒数的认识》教学设计之一—

了解站长

关于本站

返回老站

中国桥站

　　老百晓在线

第十一册

倒数的认识

教学设计

	作者：佚名
	《倒数的认识》教学设计之一

　　教学目标：
　　1、使学生理解倒数的意义，掌握求一个数的倒数的方法。
　　2、培养学生观察、归纳、推理和概括的能力。
　　3、培养学生严谨好学的学习态度。
　　重点难点：
　　重点：理解倒数的意义。
　　难点：掌握求倒数的方法。
　　教学过程：

　　一、创设情境
　　1、创设问题情境，确定研究主题
　　师：在以前的学习过程中，天天与数打交道，并且总结出关于数的运算的一些非常重要的规律，比如：一个数和1相乘还得原数；一个数和0相乘结果还是0；一个不是0的数除以它本身结果得1；??这些运算中都有着非常稳定的规律，说明两个数的关系比较稳定。今天我们就来继续研究两个数的关系。出示：
　　

　　请大家思考：每组中的两个数有怎样的关系？（生交流汇报）
　　生1：每组中都是一个真分数和一个假分数。
　　生2：两个数的分子和分母的位置正好颠倒了。
　　生3：它们的乘积都是1。
　　师：看来大家已经透过表面现象发现了两个数的本质关系，即乘积都是1。请大家逐个验证一下。
　　2、学生举例，丰富体验。
　　　请大家自己举出这样的例子。
　　3、提炼概念。
　　师：通过刚才的研究，具有这种关系的数叫互为倒数。谁来具体说一说什么样的两个数叫做互为倒数？（根据学生的回答出示：乘积是1的两个数叫互为倒数。）
　　二、加深理解
　　师：乘积是1的两个数叫互为倒数，在这个概念中你认为哪个词比较关键？为什么？自己思考后再和小组的同学交流。
　　（小组交流后汇报）
　　组1：“互为”非常关键。
　　师：“互为”是什么意思？
　　组1：“互为”是说一个数是另一个数的倒数，不能说某一个数是倒数。
　　比如：

和

中，不能说

是倒数，应该说

是

的倒数，即要说清楚谁是谁的倒数。
　　师：还可以怎么说？
　　组1：

是

的倒数。
　　组2：我们组认为“两个”这个词非常关键，必须是两个数。
　　师：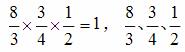

成倒数关系吗？
　　组2：不成，因为我们研究的是两个数的关系，多了不行。
　　组3：我们组认为“乘积是1”非常关键。如果乘积不是1的两个数就不能称为“互为倒数”。
　　师：通过刚才的交流，大家已经找到了在这个概念中特别关键的部分，那就是“乘积是1”、“两个数”、“互为”。
　　师：老师给大家提一个问题：概念中的“两个数”有可能是两个怎样的数？你能举例说明吗？再次小组讨论。
　　组4：有可能是两个分数，也有可能是一个整数和一个小数，或者整数和分数，只要乘积是1就行。
　　三、探究方法
　　1、探究找一个数的倒数的方法。
　　（1）师：刚才同学们都举出了许多倒数的例子。现在老师来考考你们，看看谁能很快的找出互为倒数的两个数，并说说是怎样找的？
　　出示例1。
　　生汇报结果：
　　生1：我找到了，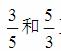

互为倒数，

互为倒数。我的方法是看这两个分数的分子和分母是不是颠倒了位置。
　　生2：我有补充，

和6也互为倒数。我是看两个数的乘积是否为1。
　　师：说说你的理由。
　　生2：我们要判断两个数是否互为倒数，就要看它们是否符合倒数的概念，也就是两个数的乘积是否为1，因为

和6的乘积也是1，所以

和6也互为倒数。
　　师：都回答的很好，看来你们对“倒数”理解得很透彻。那你更喜欢哪种方法呢？
　　生3：第一种方法，因为比较简便，一眼就可以判断。
　　生4：我也喜欢第一种，因为它比较快。师小结：看来大家都喜欢用直接观察的方法来判断，也就是看这两个分数的分子和分母是不是交换了位置。
　　（2）同学们都会判断两个数是否互为倒数了吗？如果给你一个数，你能写出它的倒数吗？
　　生齐说：能。
　　师板书：

　　生汇报方法：
　　生1：我把分子、分母的位置交换一下，就写出了

的倒数

。
　　师板书：

　　师：你们的方法和他的一样吗？
　　生齐答：一样。
　　师：谁能写出2的倒数？并说说你的方法。
　　生2:2的倒数是

。我是先把2写成分数形式

，再交换分子、分母的位置，就找出了2的倒数是

。
　　师：你真聪明！能灵活运用知识。在找整数的倒数时，我们可以先把这个整数写成分数形式，再交换分子、分母的位置的方法找出这个整数的倒数。
　　师板书：

　　师：谁能说说0.3有没有倒数？有的话怎么写出它的倒数？
　　生3：有倒数，和0.3的乘积等于1的那个数就是它的倒数。在找小数的倒数时，可以先将小数化成分数，然后交换分子、分母的位置找出这个小数的倒数。
　　师板书：

　　2、出示特例，深入理解。
　　师：刚才我们找出了例1中互为倒数的两个数，还学会了找一个数的倒数的方法。请同学们看一看，例1中还有哪些数没有找到倒数？
　　生：1和0。
　　师：1和0有没有倒数？如果有，是多少呢？请同学们讨论一下。
　　小组汇报：
　　（1）关于1的倒数。
　　组1：我们认为1有倒数，并且1的倒数还是1。因为根据倒数的意义，1×1＝1，所以说1的倒数还是1。
　　组2：我们也同意他们组的看法。我们采用了刚才学习的求整数的倒数的方法，把1写成分数形式，再交换分子、分母的位置，得到数还是1，所以说1的倒数是它本身。
　　（2）关于0的倒数。
　　组3：我们组讨论的结果是：0没有倒数，因为0乘以任何数都得0，不可能得1，不符合倒数的定义。
　　组4：我们组是这样想的：0可以写成

的分数形式来找倒数，交换分子、分母的位置后，分子是1，分母就成了0，而分母不能为0，所以0没有倒数。
　　师小结：看来同学们通过自己的努力，不仅能找到答案，还能解释原因。1和0这两个数的倒数比较特殊：1的倒数还是1,0没有倒数。
　　四、应用知识
　　1、完成“做一做”。
　　　先独立完成，再全班交流订正。
　　2、合作练习。
　　　同桌两人中的一人任意说一个数，另一个同学说出这个数的倒数，然后交换进行。
　　3、“练习六”第2题。
　　　先让学生判断对错，并说出理由。对于第（4）题“一个数的倒数一定比这个数小”，可以让学生进一步探究：什么数的倒数一定比这个数小？什么数的倒数一定比这个数大？什么数的倒数等于这个数？
　　　使学生通过讨论明确：大于1的假分数的倒数一定比它本身小，真分数的倒数一定比它本身大，1的倒数是它本身。
　　五、全课总结
　　总结：同学们这节课学得很好，不仅知道了什么是倒数，还找出了求一个数的倒数的方法：把一个数的分子、分母交换位置就可以得到这个数的倒数，并且发现了两个特殊的数：1的倒数是它本身，0没有倒数。希望同学们在以后的学习中，能坚持善于观察、勤于动脑的好习惯，掌握更多的数学知识。

　　板书设计：
　　　　　　倒数的认识

　　

　　乘积是1的两个数互为倒数
　　找倒数的方法：
　　①分数：分子、分母交换位置
　　②整数或小数：先化成分数，再交换分子、分母交换位置
　　“1”的倒数是“1”，“0”没有倒数

　　教学反思：
　　课上我主要通过体验、研究、类推等活动，使学生理解倒数的意义。在活动中，我始终以学生为主体，鼓励他们独立总结出求倒数的方法，培养他们自主学习和发展创新的意识。

[2020-11-18]

　摘自《百度文库》网站


	上一篇
	下一篇